Helligkeit der Sterne
Die Helligkeit der Sterne kann auf verschiedene Art und Weise gemessen werden. Die wichtigsten Angaben sollen hier kurz beschrieben werden.
Scheinbare Helligkeit
Schon mit dem bloßem Auge sieht man, dass die Sterne unterschiedliche Helligkeiten haben. Was wir sehen, ist die scheinbare Helligkeit der Sterne. Scheinbar deshalb, weil diese zunächst nichts über die tatsächliche oder wahre Leuchtkraft der Sterne aussagt. Die Sterne leuchten nämlich nicht alle gleich stark, sondern es gibt hell und schwach leuchtende Sterne.

Am Nachthimmel sehen wir mit bloßem Auge
die scheinbare Helligkeit der Sterne.
Fotomontage mit Sternenhimmel aus Stellarium
© Mario Lehwald
Die scheinbare Helligkeit der Sterne wird in sogenannten Größenklassen angegeben. Es gibt wie beim Thermometer einen Nullpunkt, eine positive und eine negative Seite. Hinter der Angabe der Größenklasse wird ein kleines m gesetzt (m), was Magnitudo bedeutet, dem lateinischen Wort für Größenklasse.
Der Stern Wega im Sternbild Leier hat z. B. die scheinbare Helligkeit 0m. Mit zunehmender Größenklasse nimmt die Helligkeit ab. So haben die Sterne im großen Wagen eine Helligkeit um 2m. Die Abnahme der Helligkeit ist logarithmisch, wobei der Unterschied zwischen zwei Größenklassen 2,512 beträgt. Ein Stern der Größenklasse 1m ist 2,512 mal heller als ein Stern der Größenklasse 2m und 2,512 mal 2,512 = 6,31 mal heller als ein Stern der Größenklasse 3m.
Der Unterschied zwischen 5 Größenklasse beträgt genau 100. Ein Stern der Größenklasse 0m ist also 100mal heller als ein Stern der Größenklasse 5m.
Die schwächsten Sterne, die man bei mondloser Nacht fernab der Städte noch gerade mit dem bloßem Auge sehen kann, haben die Größenklasse 6m. Mit einem guten Feldstecher kommt man etwa bis zur Größenklasse 10m, mit einem Teleskop von 15 cm Objektivdurchmesser bis knapp 13m. Professionelle Großteleskope kommen fotografisch unter die Größenklasse 30m !
Die folgende Tabelle nennt die Größenklassen und das dazugehörige optische Instrument, mit der man die entsprechende Größenklasse gerade noch sehen kann. In der mittleren Spalte ist angegeben, um wieviel schwächer ein Stern der entsprechenden Größenklasse im Vergleich zu einem Stern der Größenklasse 0 ist.
| mag | Unterschied zu 0 mag | Sichtbar mit |
|---|---|---|
| 00 | 0 | Bloßes Auge |
| 01 | 2,512 | |
| 02 | 6,31 | |
| 03 | 15,85 | |
| 04 | 39,81 | |
| 05 | 100 | |
| 06 | 251 | |
| 07 | 631 | Feldstecher |
| 08 | 1.585 | |
| 09 | 3.982 | |
| 10 | 10.002 | Teleskop 6 cm |
| 11 | 25.125 | Teleskop 7 cm |
| 12 | 63.115 | Teleskop 10 cm |
| 13 | 158.546 | Teleskop 15 cm |
| 14 | 398.269 | Teleskop 25 cm |
| 15 | 1.000.452 | Teleskop 40 cm |
| 16 | 2.513.136 | Teleskop 60 cm |
| 17 | 6.312.997 | Teleskop 100 cm |
| 18 | 15.858.250 | Teleskop 170 cm |
| 19 | 39.835.923 | Teleskop 250 cm |
| 20 | 100.067.840 | Teleskop 400 cm |
| 21 | 251.370.414 | Teleskop 600 cm |
| 22 | 631.442.480 | Teleskop 800 cm |
| 23 | 1.586.183.511 | Riesenteleskope unter Anwendung langbelichteter Fotografie
Das Hubble Weltraumteleskop kommt bis 31 mag. |
| 24 | 3.984.492.982 | |
| 25 | 10.009.046.371 | |
| 26 | 25.142.724.484 | |
| 27 | 63.158.523.903 | |
| 28 | 158.654.212.046 | |
| 29 | 398.539.380.661 | |
| 30 | 1.001.130.924.221 | |
| 31 | 2.514.840.881.644 | |
| 32 | 6.317.280.294.690 | Wird vermutlich mit dem geplanten E-ELT (42 Meter Spiegeldurchmesser!) erreicht |
| 33 | 15.869.008.100.261 | |
| 34 | 39.862.948.347.857 | |
| 35 | 100.135.726.249.817 |
Da es noch hellere Objekte wie den Stern Wega am Himmel gibt, ist die Größenklassenskala in den negativen Bereich erweitert. Der hellste Stern am Himmel überhaupt, der Sirius, hat eine scheinbare Helligkeit von -1,5m. Die Venus bringt es zu Zeiten ihrer größten Helligkeit auf -4,5m, der Vollmond auf -12,5m und die Sonne auf etwa -27m!
Absolute Helligkeit
Was wir am Himmel sehen, ist die scheinbare Helligkeit der Sterne. Um die wahre Helligkeit oder absolute Leuchtkraft der Sterne zu erhalten, müßten sie alle in der gleichen Entfernung stehen. Man hat eine solche Standardentfernung auf 32,6 Lichtjahre = 10 Parsec festgelegt.
Ist die Entfernung eines Sterns bekannt, kann man mit Hilfe der scheinbaren Helligkeit die Helligkeit berechnen, welche der Stern in einer Entfernung von 32,6 Lichtjahren hätte. Dies ist die wahre oder absolute Leuchtkraft eines Sterns. Sie wird ebenfalls in Magnitudo angegeben, aber damit es keine Verwechslung mit der scheinbaren Helligkeit gibt, wird hinter dem Helligkeitswert ein großes M (M) gesetzt. Die absolute Helligkeit unserer Sonne beträgt z. B. 4,8M. Wäre unsere Sonne 32,6 Lichtjahre von uns entfernt, würde sie nur noch als schwacher Stern der Helligkeit 4,8M am Himmel leuchten!
Bolometrische Helligkeit
Bei Angabe einer Helligkeit ist es sinnvoll, den Wellenlängenbereich anzugeben, in dem diese Helligkeit gemessen wurde. Dies kann z. B. der Bereich des sichtbaren Lichtes sein. In diesem Fall lautet die Einheit mv für die scheinbare, und Mv für die absolute Helligkeit. Das v steht hier für visuell.
Sterne strahlen aber noch in anderen Wellenlängenbereichen ab, z. B. im Ultravioletten, Infraroten, den Röntgen- oder Gammabereich. Daher hat man eine Bolometrische Helligkeit eingeführt, welche die Gesamthelligkeit eines Sterns in allen Wellenlängenbereichen erfaßt. Sie wird mit dem Symbol mbol für die scheinbare, und mit Mbol für die absolute Helligkeit gekennzeichnet.
Farbindex
Früher wurde zwischen visuellen und fotografischen Helligkeiten der Sterne unterschieden. Die visuelle Helligkeit ist die Helligkeit eines Sterns, die das menschliche Auge warnimmt. Die fotografische Helligkeit ist die Helligkeit, die eine blauempfindliche Fotoplatte registriert.
Heute wird das von von Harold L. Johnson (1921-1980) und William Wilson Morgan eingeführte UBV-System (Dreifarbenfotometrie) benutzt. Bei ihm wird die scheinbare Helligkeit eines Sterns in drei verschiedenen Spektralbereichen oder Wellenlängen gemessen:
- U: Scheinbare Helligkeit im Ultravioletten bei 3650 Angström
- B: Scheinbare Helligkeit im Blauen bei 4400 Angström
- V: Scheinbare Helligkeit im Gelben bei 5500 Angström (V = visuell)
Die gemessenen Helligkeiten werden in mag angegeben. Der Nullpunkt liegt bei der Spektralklasse A0. Dann sind die Helligkeitswerte für U, B und V gleich groß.
Sind alle drei Helligkeitswerte von einem Stern gemessen, werden Differenzen gebildet, und zwar U-B, U-V und B-V. Im visuellen Bereich hat der Wert B-V die meiste Bedeutung.
Ein roter Stern hat z. B. bei V (Gelb) einen höheren Helligkeitswert (kleinere Zahl!) als für B (Blau). Es wird hier also von einer größeren Zahl für B eine kleinere für V abgezogen. Das Ergebnis ist daher ein positiver Wert.
Ein blauer Stern hat dagegen einen höheren Helligkeitswert bei B (kleinere Zahl) als bei V. Es wird hier von einer kleineren Zahl für B eine größere für V abgezogen. Das Ergebnis ist daher ein negativer Wert. Bei der Spektralklasse A0 (weiß) betragen die Werte für B-V, sowie auch U-B und U-V genau 0,00.
Die Sonne mit der Spektralklasse G2 hat einen Farbindex von +0,65 und leuchtet gelblich, Rigel im Sternbild Orion ist mit -0,66 ein blauer Stern und Beteigeuze mit +1,85 ein roter Stern. Die folgende Tabelle nennt einige Werte für die hellsten Sterne:
| Stern | Stb | Name | B-V | U-B | V-R | R-I | Spektral |
|---|---|---|---|---|---|---|---|
| α | Aql | Altair | 0,22 | 0,09 | 0,14 | 0,13 | A7 V |
| α | Aur | Capella | 0,80 | 0,45 | 0,60 | 0,44 | G5 III |
| α | Boo | Arcturus | 1,23 | 1,28 | 0,98 | 0,65 | K1 III |
| α | Cas | Schedar | 1,17 | 1,12 | 0,78 | 0,60 | K0 IIIa |
| α | CMa | Sirius | 0,00 | -0,05 | 0,00 | -0,13 | A1 Vm |
| α | CMi | Prokyon | 0,42 | 0,03 | 0,42 | 0,23 | F5 IV-V |
| α | Cyg | Deneb | 0,09 | -0,23 | 0,11 | 0,10 | A2 I |
| α | Gem | Castor | 0,04 | 0,01 | 0,07 | 0,01 | A2 Vm |
| β | Gem | Pollux | 1,00 | 0,86 | 0,75 | 0,50 | K0 IIIb |
| α | Leo | Regulus | -0,11 | -0,36 | -0,02 | -0,10 | B7 V |
| α | Lyr | Wega | 0,00 | 0,00 | -0,04 | -0,03 | A0 Va |
| α | Ori | Beteigeuze | 1,89 | 2,07 | 1,57 | 1,28 | M1-2Ia |
| β | Ori | Rigel | -0,03 | -0,66 | 0,00 | -0,02 | B8 I |
| α | Per | Mirfak | 0,48 | 0,39 | 0,45 | 0,33 | F5 Ib |
| β | Per | Algol | -0,05 | -0,37 | 0,04 | -0,03 | B8 V |
| α | PsA | Fomalhaut | 0,09 | 0,06 | 0,05 | 0,02 | A3 V |
| α | Sco | Antares | 1,84 | 1,33 | 1,55 | 1,23 | M1,5I |
| α | Tau | Aldebaran | 1,54 | 1,92 | 1,23 | 0,94 | K5 III |
| α | Vir | Spica | -0,23 | -0,94 | -0,09 | -0,24 | B1 III-IV |
Dieses System wurde später auf das UBVRI-System erweitert. In diesem sind die scheinbaren Helligkeiten von zwei weiteren Spektralbereichen hinzugefügt:
- R: Scheinbare Helligkeit im Roten bei 7.200 Angström
- I: Scheinbare Helligkeit im Infraroten bei 9.000 Angström
Daraus werden dann die Differenzen U-B, B-V, V-R und R-I gebildet, wie sie auch in der Tabelle oben vorhanden sind.
Farb-Exzess
Durch interstellaren Staub wird das Licht absorbiert, wobei das kurzwellige blaue Licht stärker absorbiert wird als das langwellige rote. Das Licht wird also gerötet, wobei dieser Effekt mit zunehmender Entfernung stärker wird. Dies bezeichnet man als interstellare Extinktion.
Bildet man die Differenz zwischen dem gemessenen Wert B-V und dem wirklichen Wert B-V0, so erhält man den Farb-Exzess E(B-V):
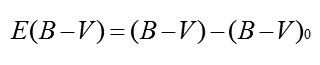
Farbindex und Spektralklasse
Die folgende Tabelle nennt den Farbindex B-V für jede Spektralklasse für Sterne der Leuchtkraftklassen V (Hauptreihensterne), IV-V, IV, III-IV und III. Datenquelle: The Intrinsic Colours of Stars and Two-Colour Reddening Lines (Fitzgerald, M. P.)
| Spekt. | Farbindex B-V | ||||
|---|---|---|---|---|---|
| V | IV-V | IV | III-IV | III | |
| O5 | -0.32 | ||||
| O6 | -0.32 | ||||
| O7 | -0.32 | ||||
| O7.5 | -0.31 | ||||
| O8 | -0.31 | -0.31 | |||
| O9 | -0.31 | -0.31 | -0.31 | -0.31 | -0.31 |
| O9.5 | -0.30 | -0.30 | -0.30 | -0.30 | -0.30 |
| B0 | -0.30 | -0.30 | -0.30 | -0.30 | -0.30 |
| B0.5 | -0.28 | -0.28 | -0.28 | -0.28 | -0.28 |
| B1 | -0.26 | -0.26 | -0.26 | -0.26 | -0.26 |
| B1.5 | -0.25 | -0.25 | -0.25 | -0.25 | -0.25 |
| B2 | -0.24 | -0.24 | -0.24 | -0.24 | -0.24 |
| B2.5 | -0.22 | -0.22 | -0.22 | -0.22 | -0.22 |
| B3 | -0.20 | -0.20 | -0.20 | -0.20 | -0.20 |
| B4 | -0.18 | -0.18 | -0.18 | -0.18 | -0.18 |
| B5 | -0.16 | -0.16 | -0.16 | -0.16 | -0.16 |
| B6 | -0.14 | -0.14 | -0.14 | -0.14 | -0.14 |
| B7 | -0.13 | -0.13 | -0.13 | -0.12 | -0.12 |
| B8 | -0.11 | -0.10 | -0.10 | -0.10 | -0.10 |
| B9 | -0.07 | -0.07 | -0.07 | -0.08 | -0.08 |
| B9.5 | -0.04 | -0.04 | -0.04 | -0.05 | -0.05 |
| A0 | -0.01 | -0.02 | -0.02 | -0.03 | -0.03 |
| A1 | 0.02 | 0.01 | 0.00 | 0.01 | 0.01 |
| A2 | 0.05 | 0.06 | 0.06 | 0.05 | 0.05 |
| A3 | 0.08 | 0.09 | 0.09 | 0.09 | 0.09 |
| A4 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 |
| A5 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| A7 | 0.20 | 0.22 | 0.22 | 0.22 | 0.24 |
| A8 | 0.27 | 0.27 | 0.26 | 0.26 | 0.26 |
| A9 | 0.30 | 0.30 | 0.29 | 0.29 | 0.28 |
| F0 | 0.32 | 0.30 | 0.30 | 0.30 | 0.32 |
| F1 | 0.34 | 0.34 | 0.33 | 0.33 | 0.33 |
| F2 | 0.35 | 0.38 | 0.37 | 0.37 | 0.36 |
| F3 | 0.41 | 0.39 | 0.39 | 0.39 | 0.39 |
| F4 | 0.42 | 0.40 | 0.42 | 0.42 | 0.42 |
| F5 | 0.45 | 0.42 | 0.44 | 0.43 | 0.43 |
| F6 | 0.48 | 0.48 | 0.46 | 0.46 | 0.46 |
| F7 | 0.50 | 0.49 | 0.50 | 0.49 | 0.48 |
| F8 | 0.53 | 0.51 | 0.53 | 0.52 | 0.52 |
| F9 | 0.56 | 0.56 | 0.57 | ||
| G0 | 0.60 | 0.60 | 0.63 | 0.62 | 0.64 |
| G1 | 0.62 | 0.60 | 0.63 | 0.69 | |
| G2 | 0.63 | 0.60 | 0.64 | 0.77 | |
| G3 | 0.65 | 0.60 | 0.66 | 0.85 | |
| G4 | 0.66 | 0.64 | 0.68 | 0.88 | |
| G5 | 0.68 | 0.68 | 0.70 | 0.85 | 0.90 |
| G6 | 0.72 | 0.73 | 0.92 | ||
| G7 | 0.73 | 0.76 | 0.94 | ||
| G8 | 0.74 | 0.80 | 0.82 | 0.89 | 0.95 |
| G9 | 0.76 | 0.83 | 0.90 | 0.95 | 0.98 |
| K0 | 0.81 | 0.86 | 0.91 | 1.01 | 1.01 |
| K1 | 0.86 | 0.93 | 0.99 | 1.09 | 1.09 |
| K2 | 0.92 | 1.16 | |||
| K3 | 0.95 | 1.26 | |||
| K4 | 1.00 | 1.43 | |||
| K5 | 1.15 | 1.51 | |||
| K7 | 1.33 | 1.53 | |||
| K9 | 1.37 | 1.55 | |||
| M0 | 1.37 | 1.57 | |||
| M0.5 | 1.47 | ||||
| M1 | 1.47 | 1.60 | |||
| M2 | 1.47 | 1.60 | |||
| M3 | 1.47 | 1.60 | |||
| M3.5 | 1.47 | ||||
| M4 | 1.52 | 1.63 | |||
| M4.5 | 1.52 | ||||
| M5 | 1.61 | 1.65 | |||
| M6 | 1.64 | 1.49 | |||
| M7 | 1.68 | 1.50 | |||
| M8 | 1.77 | 1.50 | |||
Die folgende Tabelle nennt den Farbindex B-V für jede Spektralklasse für Sterne der Leuchtkraftklassen II-III, II, Ib, Iab und Ia. Datenquelle: The Intrinsic Colours of Stars and Two-Colour Reddening Lines (Fitzgerald, M. P.)
| Spekt. | Farbindex B-V | ||||
|---|---|---|---|---|---|
| II-III | II | Ib | Iab | Ia | |
| O5 | |||||
| O6 | |||||
| O7 | |||||
| O7.5 | |||||
| O8 | -0.29 | ||||
| O9 | -0.31 | -0.31 | -0.28 | -0.28 | -0.28 |
| O9.5 | -0.30 | -0.30 | -0.27 | -0.27 | -0.27 |
| B0 | -0.30 | -0.29 | -0.24 | -0.24 | -0.24 |
| B0.5 | -0.30 | -0.28 | -0.22 | -0.22 | -0.22 |
| B1 | -0.28 | -0.24 | -0.19 | -0.19 | -0.19 |
| B1.5 | -0.27 | -0.22 | -0.17 | -0.18 | -0.18 |
| B2 | -0.22 | -0.21 | -0.16 | -0.17 | -0.17 |
| B2.5 | -0.20 | -0.19 | -0.15 | -0.15 | -0.15 |
| B3 | -0.18 | -0.17 | -0.13 | -0.13 | -0.13 |
| B4 | -0.11 | ||||
| B5 | -0.15 | -0.14 | -0.09 | -0.09 | -0.09 |
| B6 | -0.13 | -0.12 | -0.07 | -0.07 | -0.07 |
| B7 | -0.12 | -0.12 | -0.04 | -0.04 | -0.04 |
| B8 | -0.10 | -0.10 | -0.02 | -0.02 | -0.01 |
| B9 | -0.08 | -0.06 | -0.02 | 0.00 | 0.00 |
| B9.5 | -0.04 | -0.03 | -0.01 | 0.00 | 0.01 |
| A0 | -0.01 | 0.00 | 0.00 | 0.01 | 0.02 |
| A1 | 0.02 | 0.03 | 0.03 | ||
| A2 | 0.05 | 0.05 | 0.05 | ||
| A3 | 0.06 | 0.06 | |||
| A4 | 0.08 | 0.08 | |||
| A5 | 0.13 | 0.10 | 0.10 | 0.10 | 0.10 |
| A7 | 0.14 | 0.13 | 0.13 | 0.13 | |
| A8 | 0.14 | 0.14 | 0.14 | ||
| A9 | 0.18 | 0.14 | 0.14 | 0.14 | |
| F0 | 0.15 | 0.15 | 0.15 | ||
| F1 | 0.16 | 0.16 | 0.16 | ||
| F2 | 0.18 | 0.18 | 0.18 | ||
| F3 | |||||
| F4 | |||||
| F5 | 0.38 | 0.26 | 0.26 | 0.26 | |
| F6 | |||||
| F7 | |||||
| F8 | 0.55 | 0.55 | 0.55 | ||
| F9 | |||||
| G0 | 0.73 | 0.82 | 0.82 | 0.82 | |
| G1 | 0.80 | 0.85 | 0.85 | 0.85 | |
| G2 | 0.87 | 0.88 | 0.88 | 0.88 | |
| G3 | 0.86 | 0.87 | 0.92 | 0.92 | 0.92 |
| G4 | 0.87 | 0.87 | |||
| G5 | 0.88 | 0.87 | 1.00 | 1.00 | 1.00 |
| G6 | 0.92 | 0.91 | 1.04 | 1.04 | 1.04 |
| G7 | 0.94 | 0.95 | 1.10 | 1.10 | 1.10 |
| G8 | 0.96 | 0.99 | 1.14 | 1.14 | 1.14 |
| G9 | 1.00 | 1.02 | 1.16 | 1.16 | 1.16 |
| K0 | 1.05 | 1.06 | 1.18 | 1.18 | 1.18 |
| K1 | 1.10 | 1.14 | 1.20 | 1.20 | 1.20 |
| K2 | 1.13 | 1.29 | 1.23 | 1.23 | 1.23 |
| K3 | 1.30 | 1.40 | 1.42 | 1.42 | 1.42 |
| K4 | 1.50 | 1.42 | 1.50 | 1.50 | 1.50 |
| K5 | 1.57 | 1.45 | 1.60 | 1.60 | 1.60 |
| K7 | 1.57 | 1.62 | 1.62 | 1.62 | |
| K9 | 1.58 | 1.58 | 1.64 | 1.64 | 1.64 |
| M0 | 1.58 | 1.58 | 1.65 | 1.65 | 1.65 |
| M0.5 | |||||
| M1 | 1.60 | 1.59 | 1.65 | 1.65 | 1.65 |
| M2 | 1.60 | 1.59 | 1.65 | 1.65 | 1.65 |
| M3 | 1.60 | 1.60 | 1.67 | 1.67 | 1.67 |
| M3.5 | |||||
| M4 | 1.75 | 1.75 | 1.75 | ||
| M4.5 | |||||
| M5 | |||||
| M6 | |||||
| M7 | |||||
| M8 | |||||